
Toposes in Mondovì
Toposes in Mondovì
Topos theory can be regarded as a unifying subject within Mathematics; in the words of Alexander Grothendieck, who invented the concept of topos, “It is the theme of toposes which is this “bed”, or this “deep river”, in which come to be married geometry and algebra, topology and arithmetic, mathematical logic and category theory, the world of the continuous and that of the “discontinuous” or “discrete” structures. It is what I have conceived of most broad, to perceive with finesse, by the same language rich of geometric resonances, an “essence” which is common to situations most distant from each other, coming from one region or another of the vast universe of mathematical things.
The event “Toposes in Mondovì” (3-11 September 2024) represents the fourth edition of the main international conference on topos theory, following the previous ones “Topos à l’IHES” (2015), “Toposes in Como” (2018) and “Toposes online” (2021).
The format of the event is similar to that of the other three editions: it will consist of a four-day school (3-6 September 2024) offering introductory courses for the benefit of students and mathematicians who are not already familiar with topos theory, followed by a three-day conference (9-11 September 2024) featuring both invited and contributed presentations on new theoretical advances in the subject as well as applications of toposes in different fields such as algebra, topology, number theory, algebraic geometry, logic, homotopy theory, functional analysis, and computer science.
The main aim of this conference series is to celebrate the unifying power and interdisciplinary applications of toposes and encourage further developments in this spirit, by promoting exchanges amongst researchers in different branches of mathematics who use toposes in their work and by introducing a new generation of scholars to the subject.

School lecturers
- Marc Aiguier (CentraleSupélec, Université Paris-Saclay)
- Olivia Caramello (University of Insubria and Grothendieck Institute)
- Alain Connes (IHES and Collège de France)
- Denis-Charles Cisinski (University of Regensburg)
- Dennis Gaitsgory (Max Planck Institute for Mathematics)
- Laurent Lafforgue (Huawei)
- Michael Robinson (American University)
- Isar Stubbe (Université du Littoral-Côte d’Opale)
Invited speakers
- Joseph Bernstein (Tel Aviv University)
- Paolo Giordano (University of Vienna)
- Peter Haine (University of California, Berkeley)
- Matthias Hutzler (University of Gothenburg)
- Asgar Jamneshan (Koç University)
- Maxim Kontsevich (IHES)
- Hugo Luiz Mariano (University of São Paulo)
- Axel Osmond (Grothendieck Institute)
- Hans Riess (Duke University)
- Michael Shulman* (University of San Diego)

* online participation
Mondovì
Mondovì is a beautiful town located in Piedmont, northern Italy, in the Langhe territory, close to the French border, about 80 km from the city of Turin and at 80 km from the Ligurian sea.
Mondovì was founded on a hilltop in 1198 as an independent ‘comune‘ (township). It continued to grow until the 16th century when it became the largest city in Piedmont. In 1537 it was occupied by France, under which it mostly remained until 1559. In 1560, Emmanuel Philibert, Duke of Savoy restored it to Piedmont, which held it until the Italian unification, apart from the Napoleonic period (1796–1814).
Mondovì has been known as the ‘City of Studies’ since the period from 1560 to 1566, when the city was the seat of Piedmont’s first university with the right to confer degrees in various disciplines.
Today Mondovì is the seats of several academic and cultural institutions, including, besides the Grothendieck Institute, the internationally acclaimed baroque orchestra and musical university Academia Montis Regalis, the Polytechnic University of Turin (secondary pole) and the Arts University Academia Cirko Vertigo.
School and conference venues
The school of “Toposes in Mondovì” will take place in the lower part of the Mondovì, while the conference will be held in the upper part, the two being directly connected by a funicular.
School location:
Aula Magna – Mondovì site of the Polytechnic University of Turin
Via San Giuseppe Benedetto Cottolengo, 29
12084 Mondovì – CN, Italy
The Mondovì seat of the Polytechnic University of Turin is a place rich in history. Originally, from September 1574 until 1931, the building was used as the Hospital of St Francis of Assisi. In the second half of the 1980s, the building hosted a primary school and secondary school branch.
Later, with the growing demand for a university-technological reference point, it became the seats of the Polytechnic University of Turin in 1990. This transformation revived Mondovì’s ancient tradition as a ‘City of Studies’, dating back to the period from 1560 to 1566, when the city was the seat of a university with the right to confer degrees in various disciplines.

HOW TO GET THERE:
The Polytechnic University of Turin – Mondovì site is 10 minutes by foot from the lower historical centre, and 20 minutes by foot from the Mondovì railway station. From the station, you can also take buses (lines 2 or 3), getting off at the stop ‘Piazzetta Levi’; from there the site can be reached by foot in 10 minutes.

Conference location:
Circolo di Lettura – Palazzo del Governatore
Via Francesco Gallo, 1
12084 Mondovì – CN, Italy
The conference will be hosted in the prestigious Governor’s Palace in the upper historical centre, nowadays the seats of the Circolo di Lettura. The palace was originally built in the 15th century. Characterised by the presence of a portico with pointed arches on the ground floor and outstanding frescos on the entire surface of the external façade as well as in the interiors, the palace has been the seat of power of the Savoy family. From the 15th century, the facade was painted with various emblems and coats of arms, and in particular with the coats of arms of the governors and the families who ruled the city.
The recent restoration has returned the extraordinary repertoire of coats of arms and emblems that testify to almost five hundred years of the city’s history.
HOW TO GET THERE:
The two historical centres are well connected by the local public transportation lines (from Mondovì railway station, the nearest bus stop to catch is in front of it – line 2 or 3 – and the bus stop is ‘Piazza Maggiore’) and by a modern and functional funicular railway, between the lower and upper district (Piazza).
The entrance of the Governor’s Palace is very close, on the other side of the square.
School courses
Marc Aiguier (CentraleSupélec, Université Paris-Saclay)
Logic, categories and topos: from category theory to categorical logic
Mathematical logic as the foundation of mathematics was first studied in the set-theoretic framework. Following Grothendieck’s works on topos in the late 1950s, and the fact that the latter possessed properties that brought them closer to sets, logicians under the leadership of Lawvere proposed to extend the semantics of first-order logic and its fragments (higher-order logic, geometric logic, etc.) to category theory and among other things to a finitary axiomatization of topos, elementary topos.
The outline of this course will be as follows:
- Syntax of logics (signature, terms, formulas, sequent and theory)
- Categorical semantics (subobject, structures and evaluation of terms)
- Satisfaction of FO formulas in Heyting categories
- Lawere’s hyperdoctrines
- Elementary toposes
- Interpretation of sequents
- Kripke-Joyal semantics
- Interpretation of HOL in elementary toposes
- Geometric logic
- Geometric category
- Grothendieck toposes
- Inference systems (rules, correctness and completeness)
- Syntactic category and universal model
- Representable functor T-Mod
- Classifying topos
Video: part 1, part 2
Olivia Caramello (University of Insubria and Grothendieck Institute)
Relative toposes for the working mathematician
Relativity techniques for schemes have played a key role in Grothendieck’s refoundation of algebraic geometry. We shall give an introduction to the relativity techniques for toposes, formulated in the language of stacks and fibrations, that we have been developing since 2020.
After recalling the necessary preliminaries, we will discuss the problem of representing geometric morphisms both in terms of morphisms and comorphisms of sites; this will lead to the notion of “relative site” and the study of the associated “relative toposes”.
We will show that the usual presheaf-bundle adjunction for topological spaces generalizes to arbitrary sites, by replacing continuous maps to the space with relative toposes (with respect to the topos of sheaves on the given site).
We shall then present a generalisation of Diaconescu’s equivalence for relative toposes, formulated in the language of relative sites.
Lastly, we will introduce the concept of “existential fibred site” (a broad, site-theoretic generalisation of the notion of (hyper)doctrine), and that of “existential topos” of such a site: these notions notably allow us to develop relative topos theory in a way which naturally generalizes the construction of toposes of sheaves on locales, providing a unified framework for investigating the connections between Grothendieck toposes as built from sites and elementary toposes as built from triposes.
We shall discuss several examples and applications of the notions and results presented in the lectures, of algebraic, geometric and logical nature.
Part of the material presented in the course comes from joint works with R. Zanfa, L. Bartoli and R. Lamagna.
Video: part 1, part 2
Alain Connes (IHES)
Knots, Primes, and the Scaling Site
The topic of my course will focus on the interrelation between a very specific topos, the scaling site, and the well-known analogy going back to 1963 between knots and prime numbers.
The topos, which is the scaling site, is simple to define as the semi-direct product of the half-line of positive or zero real numbers by the action of the positive integers, by multiplication.
It turned out in 2014 (in joint work with C. Consani) that the points of this topos were identified with a space which had occurred in 1996 in non-commutative geometry related to the Riemann zeta function, and which is obtained by starting with the adele class space and dividing it by the action of the maximal compact subgroup of the Idele class group.
The main point of the class will be to understand the use of topos theory and of non-commutative geometry in order to understand the scaling site and the finite abelian covers of the scaling site associated to finite abelian extensions of the field of rational numbers.
Grothendieck, by his theory of the etale fundamental group, has extended Galois theory from the context of fields to the context of schemes.
The main new result which I will present (a joint work with C. Consani) is that the scaling site and the adele class space allow one to extend the class field theory isomorphisms, which usually relate Galois groups with groups of adelic nature, to the situation where one is no longer starting with a Galois group, but one is starting with a scheme intimately related to the field of rational numbers, and one associates to this scheme its class field theory counterpart, which can be seen either at the adelic level or at the topos level.
Video: part 1, part 2
Denis-Charles Cisinski (University of Regensburg)
Synthetic ∞-category theory and elementary ∞-topoi
We will propose a formal language of category theory, independent of set-theoretic foundations. Formally, this language is a variation of type theory, but, as for set theory, there is a “naïve” version in natural language (with which we actually work) and this is what we will introduce.
Although this language looks like (and arguably can be) the one of ordinary category theory, a suitable version of Voevodsky’s univalence axiom will turn it into the language of infinity-categories as developed by Joyal and Lurie, in a version that is expressive enough to prove all the basic results of (higher) category theory – including the theory of Grothendieck topoi.
This language also expresses (higher) category theory internally to any (higher) topos.
The goal of this lecture series is to introduce such a language and to explain why it is in fact a way to define what is an elementary topos in the setting of higher category theory.
E.Riehl, M. Shulman A type theory for synthetic ∞-categories, Higher Structures 1 (2017), 116–193
D.-C. Cisinski, Higher Categories and Homotopical Algebra, Cambridge studies in advanced mathematics, vol. 180, Cambridge University Press, 2019.
H.K.Nguyen, Covariant & Contravariant Homotopy Theories, arXiv:1908.06879.
H.K.Nguyen, A note on coCartesian fibrations, arXiv:2210.07753
D.-C. Cisinski and H. K. Nguyen, The universal coCartesian fibration, arXiv:2210.08945
B.Cnossen, Formalization of Higher Categories, based on a lecture course by D.-C. Cisinski. Available at https://sites.google.com/view/bastiaan-cnossen
Series of papers on ∞-category theory in higher topoi by L. Martini and S. Wolf
Video: part 1, part 2
Dennis Gaitsgory (Max Planck Institute for Mathematics)
2-Fourier-Mukai transform and geometric Langlands for non-constant group-schemes
Let be a curve, and
a semispmple group. Let
be the moduli stack of
-bundles on
. Let
be the Langlands-dual of
, and let
be the stack of
-local systems on
. The geometric Langlands conjecture (now a theorem) says that there is an equivalence
(*) .
(We suppress the difference between and
as it will play no role in what follows.)
Now, one can twist the two sides of (*) as follows:
(a) Using the short exact sequence
, given a gerbe
on
with respect to
,
we can form a twist of
as a group-scheme over
, and consider the category
(b) Using the short exact sequence
,
given a gerbe on
with respect to
, we can form a twist
of
as a group-scheme over
, and consider the category
.
It will turn out that the above two operations are dual to each other with respect to the operation of 2-Fourier-Mukai transform.
We will explore this relationship and its consequences for Langlands correspondence.
Video: part 1, part 2
Laurent Lafforgue (Huawei)
Geometry and logic of subtoposes
After reviewing the multiple roles of toposes – as generalized topological spaces, as universal invariants, as pastiches of the category of sets and as incarnations of the semantics of first-order theories -, we shall recall the definition of the notion of subtopos and its double expression in terms of Grothendieck topologies and in terms of first-order logic. We shall stress the consequence of this double expression for translating first-order provability problems into problems of generation of Grothendieck topologies, and we shall introduce the natural geometric inner and outer operations on subtoposes.
After introducting these themes, we shall give a new presentation – based on some very general abstract nonsense – of the duality of Grothendieck topologies and subtoposes, and of the duality of topologies and closedness properties of subpresheaves.
Then we shall present two different general formulas expressing the Grothendieck topology generated by any given family of sieves or of covering families of morphisms. We shall also make more precise the constructive processes which allow to translate provability problems into topology generation problems.
Lastly, we shall study the inner geometric operations on subtoposes – union, intersection, difference – and the outer adjoint operations of push-forward and pull-back by topos morphisms. We shall prove that pull-back operations always respect not only arbitrary intersections but also finite unions of subtoposes, and that pull-backs by “locally connected” morphisms even respect arbitrary unions of subtoposes.
Part of the material of the lecture course is classical – borrowed from SGA4, from O. Caramello’s book “Theories, Sites, Toposes” and from other references – and part is new, borrowed from a joint paper coauthored with O. C. to appear soon under the title “Engendrement de topologies, démontrabilité et opérations sur les sous-topos”.
Video: part 1, part 2
Michael Robinson (American University)
Practical systems modeling in categories using sheaves
Modeling practical systems using category theory (and especially topoi) can be daunting! There is plenty of expressive power, but in a sense it is too much. Fortunately, most practical systems also have a notion of topology, which provides strong modeling constraints. The theory of sheaves forms a functorial bridge between the topology of a model and its associated data. Famously, categories of sheaves are topoi. Therefore, although the job of modeling with sheaves is easier than purely with categories, it does not come at the expense of expressivity. Over the past decade or so, the topological data modeling community has developed tools that allow one to easily and effectively build sheaf models for common system models. This summer school session will explain how these work, both theoretically and practically.
It is also important to note that practical systems also have to deal with noise, errors, and uncertainty. Fortunately, sheaves are topological in their organization and in their representation of data. With a little forethought, sheaves can be used to handle the vagaries of practical systems. Moreover, in many scientific and engineering settings, there is geometric information. This allows one to measure how closely aligned the model posited by a sheaf and experimentally collected data are. The result is a statistical interpretation of data, models, and topology that has a practical algorithmic implementation… and this too is functorial! This summer school session will include software demonstrations to introduce participants to the use of these tools. General overview of sheaves: For building topological and sheaf models from “standard” data: From timeseries (strong neurological relevance): From the Dowker complex: Using “classical” and hybrid classical models: From networks: Practical algorithms and tools:
Video: part 1, part 2
Isar Stubbe (Université du Littoral-Côte d’Opale)
Quantaloid-enriched categories for sheaf theory
A sheaf F on a locale L is commonly defined as a contravariant Set-valued functor on L that satisfies the gluing condition. Together with natural transformations, these sheaves form the objects and morphisms of the localic topos Sh(L). While every localic topos is a Grothendieck topos, the converse does not hold—there exist Grothendieck toposes that are not localic.
For any two elements (or sections) x and y in such a sheaf F (meaning that x is in Fu, and y is in Fv, for some u,v in L), we can measure the extent to which x equals y by computing the supremum of all w below both u and v on which the restrictions of x and y are equal (in the set Fw). This L-valued map on pairs of elements of F plays the role of a characteristic function for equality. In fact, the notion of sheaf can be reformulated in terms of such an L-valued map; and (together with an appropriate notion of morphism) these ‘L-sets’ form a category equivalent to Sh(L).
This latter formulation puts sheaf theory in the realm of many-valued logic, or more specifically, of quantaloid-enriched categories – and this will be the central theme of our lectures. Concretely, we shall first define quantales and quantaloids, explore some key universal constructions on these, and discuss several examples (noting in particular that locales are precisely ‘cartesian’ quantales). Then we will explain the fundamentals of quantaloid-enriched category theory, and show its flexibility and applicability through various examples. Finally we shall indicate how every Grothendieck topos Sh(C,J) is equivalent to a category of ‘Q-sets’ for an appropriate quantale Q, thereby showing that “every Grothendieck topos is quantalic”.
Video: part 1, part 2
Invited speakers
Joseph Bernstein (Tel Aviv University)
Groups, Groupoids, Stacks and Representation Theory
In my talk I would like to introduce a new approach to Representation Theory.
Let G be an abstract group and k some field. A representation of the group G over the field k is usually defined as a pair (π, V), where V is a vector space over k and π is a morphism from G to Aut(V).
One of basic problems in Representation Theory is the study of the category Rep(G) of such representations.
In my talk I will explain that there is another natural way to describe this category.
Namely, the category Rep(G) is naturally equivalent to the category of sheaves Sh(B(G)) on some “geometric” object – the basic groupoid BG of the group G.
Thus we have two equivalent definitions of representations – standard one and categorical definition in terms of groupoids. I will explain that more sophisticated categorical description is more “correct” one. For example, it gives a more adequate description of the category Rep(G) in cases when we have some external symmetries.
The gap between these two definitions becomes much more profound when we move from the category of sets to other categories (more precisely – sites).
In this case the role of groupoids are played by stacks. So I propose to define the category of representations of a group G as the category of sheaves on the basic stack BG.
I will discuss how these things play out in the important case when G is an algebraic group over a local field.
My talk will partially follow my paper in arXiv:1410.0435. Relation between groups and groupoids is discussed in a paper by R. Brown “From Groups to Groupoids: a Brief Survey”, Bull. London Math. Soc. 19 (1987) 113-134.
Paolo Giordano (University of Vienna)
The Grothendieck topos of generalized smooth functions
The need to describe abrupt changes or response of nonlinear systems to impulsive stimuli is ubiquitous in applications. Also within mathematics, L. Hörmander stated: “In differential calculus one encounters immediately the unpleasant fact that not every function is differentiable. The purpose of distribution theory is to remedy this flaw; indeed, the space of distributions is essentially the smallest extension of the space of continuous functions where differentiability is always well defined”. We first describe the universal property of the space of distributions, but then we underscore the main deficiencies of this theory: we cannot evaluate a distribution at a point, we cannot make non-linear operations, let alone composition, we do not have a good integration theory, etc. We then present generalized smooth functions (GSF) theory, a nonlinear theory of generalized functions (GF) as used by physicists and engineers, where GF are ordinary set-theoretical maps defined on and taking values in a non-Archimedean ring extending the real field (this problem has been faced e.g. by: Schwartz, Lojasiewicz, Laugwitz, Schmieden, Egorov, Robinson, Colombeau, Rosinger, Levi-Civita, Keisler, Connes, etc.); GSF are closed with respect to composition so that nonlinear operations are possible; these operations coincide with the usual ones for smooth functions; all classical theorems of differential and integral calculus hold; we have several types of sheaf properties, and GSF indeed form a Grothendieck topos; we have a full theory of ODE, and general existence theorems for nonlinear singular PDE, e.g. the Picard-Lindelöf theorem for PDE; every Cauchy problem with a smooth PDE is Hadamard well-posed; we can generalize the classical Fourier method also to non-tempered GF (this problem has been faced e.g. by Gelfand, Sobolev); we have several applications in the calculus of variation with singular Lagrangians, elastoplasticity, general relativity, quantum mechanics, singular optics, impact mechanics (this problem has been faced by J. Marsden). We close by presenting a project in collaboration with several Japanese universities about how to apply GSF theory to have GF in diffeological spaces and hence to make homotopy theory where continuous functions can be treated as smooth functions, or to try to replicate synthetic differential geometry in the Grothendieck topos using nilpotent infinitesimals for this type of GF.
Peter Haine (University of California, Berkeley)
Reconstructing schemes from their étale topoi
In Grothendieck’s 1983 letter to Faltings that initiated the study of anabelian geometry, he conjectured that a large class of schemes can be reconstructed from their étale topoi. In this talk, I’ll discuss joint work with Magnus Carlson and Sebastian Wolf, generalizing work of Voevodsky, that proves Grothendieck’s conjecture. Specifically, we show that over a finitely generated field k of characteristic 0, seminormal finite type k-schemes can be reconstructed from their étale topoi. Over a finitely generated field k of positive characteristic and transcendence degree ≥ 1, we show that perfections of finite type k-schemes can be reconstructed from their étale topoi. Combined with joint work with Barwick and Glasman, and work of Makkai and Lurie on strong conceptual completeness, we deduce that such schemes can also be reconstructed from two different condensed categories of points of their étale topoi. Our talk will focus on the topos-theoretic aspects of these results.
Matthias Hutzler (University of Gothenburg)
Projective Space and Line Bundles in Synthetic Algebraic Geometry
Synthetic algebraic geometry is the study of schemes using an internal language of the Zariski topos. More precisely, Homotopy Type Theory (HoTT) is interpreted in a higher-topos variant of the Zariski topos in order to have a powerful language that can talk about higher homotopical objects just as easily as set-level objects. From this internal perspective, schemes such as for example projective space appear simply as certain h-sets without any added structure.
In the talk we present a synthetic version of the classical classification result for line bundles on projective space. The language of HoTT allows us to give a stronger variant of the classical statement, describing the 1-type of line bundles instead of its set-truncation, the Picard group. This is used to give a proof that requires nontrivial algebraic arguments only for the case of the projective line, and derives the general case by an interpolation argument.
Asgar Jamneshan (Koç University)
Some Applications of Toposes of Measure-Theoretic Sheaves
We construct toposes of sheaves on measure spaces and highlight the usefulness of interpreting certain structures from classical measure theory and functional analysis, combined with a Boolean internal logic, in applications to ergodic structure theory and vector duality.
Maxim Kontsevich (IHES)
What is the spectrum of quantum algebra?
For quantum algebras, like e.g. algebras of polynomial differential operators or q-difference operators, the “minimal” non-trivial modules are holonomic ones. These objects are not point-like, and correspond roughly to vector bundles on Lagrangian subvarieties in the semi-classical limit.
I’ll talk about various approaches to supports: 1) via behavior at infinity, 2) via reduction modulo large primes, 3) via multiplicative semi-norms in the non-archimedean case.
Mariano Hugo Luiz (University of São Paulo)
In this talk, we will present some recent developments associated with some PhD theses in IME-USP (Institute of Mathematics and Statistics, University of São Paulo, Brazil) on categories of sheaves over quantales and categories of quantale valued sets, returning to a theme of studies involving logic and categories carried out at IME-USP in the latter half of the 1990, but now from a new perspective: considering semicartesian and commutative quantales, as non-idempotent generalizations of locales (= complete Heyting algebras).
We will list some properties of the (monoidal) categories obtained, indicating some similarities and differences with the Grothendieck topos. The main goal of these efforts is to develop a closed monoidal but not cartesian closed generalization of the notion of elementary topos, in order to cover some mathematical situations (including generalizations of metric spaces), to enable an axiomatic study of these categories, and a general definition of their internal logic, which shows clues of being some form of linear logic.
A future goal is to establish a precise relationship between the present approach and the enriched category approach to sheaves over quantales (and quantaloids) developed by I. Stubbe.
Axel Osmond (Grothendieck Institute)
Morphisms and comorphisms of sites: double-categorical and profunctorial aspects
Geometric morphisms can be induced either from morphisms or comorphisms of sites, respectively in a contravariant and in a covariant way; the first are characterized through a cover-preservation property, the second through a cover-reflection property. As both define a relevant notion of 1-cells between sites, one may ask two questions:
- is there a proper way to mix them altogether in a single categorical structure on sites, and if so, does it help understanding the reason for which we have those twin classes of functors rather than a single one?
- is it possible to subsume them into a single notion jointly generalizing the cover-preservation and cover-reflection into a single condition?
In this talk, based on an ongoing work with Olivia Caramello, we will try to address those two questions.
In a first part, we will explain how morphisms and comorphisms, though they do not compose with each other, can be arranged as the horizontal and vertical 1-cells of a double-category of sites, and how the sheaf-topos construction defines a double-functor to the quintet double-category of topoi. We will also discuss some companion and conjoint constructions in this setting, as well as a link between this double-category of sites and the double-category of co-algebras, lax and colax morphisms for a 2-comonad.
In a second part, we will try to answer to the second question through notions of continuity for distributors (a.k.a. profunctors); building on Bénabou theory of flat distributors and refining a previous definition of Johnstone and Wraith, we prove an equivalence between continuous distributors between sites and geometric morphisms between the corresponding sheaf topoi, and discuss how this notion relates respectively to morphisms and comorphisms of sites.
Hans Riess (Duke University)
John Baez and others have noted a compelling analogy between adjoint functors in category theory and adjoints of linear operators in Hilbert spaces. This analogy is particularly striking when considering enriched adjunctions, where the hom mimics an inner product. On the other hand, Hodge theory, which bridges PDEs with geometry and topology, fundamentally relies on the existence of an adjoint operator within the de Rham complex. In this talk, we explore ongoing efforts to categorify the Hodge Laplacian, focusing on the connection Laplacian—a special case involving parallel transport between tangent spaces of a manifold. We propose a framework for parallel transport and a connection Laplacian within the setting of presheaves on preorder into the category of V-enriched categories. Finally, we outline preliminary examples of this theory, with potential applications to logic, formal concept analysis, and tropical geometry.
Michael Shulman (University of San Diego)
Internal languages of diagrams of toposes
Internal languages are a powerful tool for studying toposes, but traditionally they can only be applied to a single topos at a time, whereas frequently we are interested in a number of toposes related by a diagram of geometric morphisms. The collection of internal languages of the toposes in such a diagram, together with syntactic operations relating them corresponding to the direct and inverse image functors of the geometric morphisms and transformations, form a “modal” type theory, with the functor operations known as “modalities”. The first general modal type theories, applicable to a diagram of arbitrary shape, have recently been formulated by Gratzer, Kavvos, Nuyts, and Birkedal, but interpreting these theories in a diagram of toposes appears to require that all the geometric morphisms be essential. I will show how this requirement can be avoided, by generalizing the construction of a “fibration of sites” presenting a single geometric morphism to a presentation of an arbitrary diagram of such.
Contributed talks
Thiago Alexandre (University of São Paulo and IMJ, Paris)
The theory of derivators was originally developed by Grothendieck with high inspiration in topos cohomology. In a letter sent to Thomason, where he explains the main ideas and motivations guiding the formal reaosining of derivators, Grothendieck also remarks that those are Morita-invariant. This means that if two small categories X and Y have equivalent topoi of presheaves, then the categories D(X) and D(Y) are also equivalent for any derivator D. This observation suggests that it may be possible to extend any derivator D to the entire 2-category of topoi and geometric morphisms between them. Grothendieck speculates that such an extension is always possible and essentially unique. In this case, every derivator D defined over small categories would be coming from a derivator D’ defined over topoi via natural equivalences of categories of the form D(X) = D’(X^), for X varying through small categories and X^ denoting the category of presheaves over X. However, despite these considerations, a theory of derivators over topoi has not yet been developed. To address this gap, I am currently developing a theory of topological derivators. These derivators, defined on the 2-category of topoi, aim to provide answers to Grothendieck’s conjecture.
Beyond applications in geometry, the theory of topological derivators also offers a potential framework to connect categorical logic and homotopical algebra. In my talk, I would like to present the theory of topological derivators and some of its main results until now, including examples, some techiniques to construct topological derivators, and how topological derivators are related with the homotopy theory of topoi.
Igor Baković
(Co)Fibrations, (pseudo)distributive laws and (quasi)Toposes
Mainly motivated by the symmetric monad in toposes which classifies Lawvere’s distributions, Bunge and Funk developed the theory of admissible Kock-Zoberlein doctrines or (co)lax idempotent 2-monads. Their first main contribution is a characterization of the Eilenberg-Moore 2-category of algebras of an admissible 2-monad in terms of (co)completeness. Their second major contribution is a description of the Kleisi 2-category by means of its bifibrations which are defined by a certain bicomma object condition and the corresponding comprehensive factorization for those 1-cells which have an admissible domain.
However, besides some less known and exotic example from computer science theory, the symmetric topos was their only major example of an admissible 2-monad. In my talk, I prove that one of the most fundamental 2-monads – associated (split) fibration – is admissible. Then I show how the known case of a 2-monad whose underlying 2-functor is defined over a fixed base category extends to a 2-functor on the 2-category whose objects are functors and 1-cells are colax squares – those which commute up to an upwards pointing natural transformations. If one wants to extend the action of a 2-monad on the 2-category of lax squares – those which commute up to a downward pointing natural transformations – one needs to impose the existence of pullbacks in codomains of objects which we treat as generalized fibrations following Bénabou.
Léo Bartoli (Grothendieck Institute and ETH Zurich)
Local Fibrations and Relative Diaconescu’s Theorem
To develop relative topos theory, that is, topos theory over an arbitrary base topos, the language of stacks –or more generally, indexed categories – has proven to be very efficient. The notion of a category indexed by a base site constitutes the relative analogue of the concept of a category, and by endowing the associated fibrations with certain Grothendieck topologies, we arrive at the notion of a relative site.
In this presentation of joint work with Prof. Olivia Caramello, we first introduce a localization of the notion of fibration with respect to certain topologies (specializing to ordinary fibrations when these topologies are trivial). Indeed, it is within this broader framework that we are able to obtain a comprehensive understanding of which morphisms of sites induce morphisms of relative toposes. As in the “absolute” case, we identify a relative extension of a morphism of sites along a canonical functor (a relative analogue of the Yoneda embedding), which preserves finite limits fiberwise precisely when the functor in question induces a morphism of relative toposes. The notion of local fibrations allows for an elegant characterization of those functors that induce morphisms of relative toposes: they are precisely the morphisms of sites that also are morphisms of local fibrations.
These considerations naturally lead to the concept of a relatively flat functor, which in turn allows us to obtain a relative version of Diaconescu’s theorem for local fibrations (and hence also for ordinary fibrations), characterizing the relative geometric morphisms towards a relative sheaf topos in terms of relatively flat functors.
Claudio Fontanari (University of Trento)
Moduli spaces of curves and topos theory
According to Grothendieck, the moduli spaces of curves are among mathematical objects “les plus beaux, les plus fascinants que j’aie rencontrés” and topos theory is “fait sur mesure pour exprimer ce genre de situation” much better than the language of algebraic stacks introduced by Deligne and Mumford. In my short communication I would like to pose the following open question: “Consider the moduli spaces of curves as Grothendieck toposes. May this (more natural, at least according to Grothendieck) approach have any interesting consequence on our understanding of the geometry of these beautiful spaces?”. I am also going to propose a tentative answer, by referring to Kontsevich’s “hidden smoothness philosophy” and to derived algebraic geometry.
Ryuya Hora (University of Tokyo)
The colimit of all monomorphisms classifies hyperconnected geometric morphisms
One of the most fundamental theorems in topos theory is the correspondence theorem between subtopoi and Lawvere-Tierney topology. This theorem allows us to reduce the classification problem of subtopoi to the classification problem of idempotent internal semilattice homomorphisms on the subobject classifier.
What about the “dual case” of quotient topoi (i.e., connected geometric morphisms)? This problem is the first of Lawvere’s open problems in topos theory:
[…] Is there a Grothendieck topos for which the number of these quotients is not small? At the other extreme, could they be parameterized internally, as subtopoi are?
In this presentation, I will discuss a partial answer to this question by presenting a classification theorem for hyperconnected geometric morphisms, which are quotient topoi satisfying an additional condition. Our theorem classifies hyperconnected geometric morphisms using internal semilattice homomorphisms, similar to the case of subtopoi. We define a semilattice called the local state classifier (LSC) as the “colimit of all monomorphisms” and prove that semilattice homomorphisms LSC to the subobject classifier are in one-to-one correspondence with hyperconnected geometric morphisms.
The interesting aspect of this result lies in the fact that actual computations can be performed. Although the definition of a local state classifier is transcendental, it can be concretely constructed in the case of a Grothendieck topos. For example, for a presheaf topos over a small category, the local state classifier is the presheaf consisting of all quotient objects of the representable functors, which is dual to the construction of the subobject classifier! This talk is based on the paper “Internal Parameterization of Hyperconnected Quotients”, arXiv:2302.06851 (2023).
Giuseppe Leoncini (Masaryk University and University of Milano)
Homotopy colimits over a topos
Starting from a 1-categorical base V which is not assumed endowed with a choice of model structure (or any kind of homotopical structure), we define homotopy colimits enriched in V in such a way that: (i) for V = Set, we retrieve the classical theory of homotopy colimits, and (ii) restricting to isomorphisms as weak equivalences, we retrieve ordinary and enriched 1-colimits. We construct the free homotopy V-cocompletion of a small V-category in such a way that it satisfies the expected universal property. For V = Set, we retrieve Dugger’s construction of the universal homotopy theory on a small category C. We define the homotopy theory of internal infinity-groupoids in V as the homotopy V-enriched cocompletion of a point, and argue that V-enriched homotopy colimits correspond to weighted colimits in infinity-categories enriched in internal infinity-groupoids in V, thus providing a convenient model to perform computations. Again, taking V = Set, this retrieves the classical notions for ordinary infinity-categories. We compare our approach with some previous definitions of enriched homotopy colimits, such as those given by Shulman, Lack & Rosicky, and Vokrinek, and we show that, when the latter are defined and well behaved, they coincide with ours up to Quillen homotopy. The theory behaves well when the base of enrichment is a Grothendieck 1-topos. As an application, we give a new proof of the following fact (conjectured by Hill and recently proven by Shah): we show that the so-called genuine (or fine) homotopy theory of G-spaces is the G-equivariant homotopy cocompletion of a point.
Marco Panzeri (University of Insubria)
2-categorical constructions on classifying toposes
In this talk, based on joint work with Olivia Caramello, we provide logical descriptions of a number of fundamental constructions in the 2-category of Grothendieck toposes; more specifically, we describe geometric theories classified by weighted limits of classifying toposes and morphisms between them induced by interpretations, and apply this result to obtain logical descriptions of fibred products, comma objects, and small limit of toposes.
Iosif Petrakis (University of Verona)
Toposes with dependent and codependent arrows
We introduce dependent arrows as categorical generalisations of dependent functions over type-familes (set-families) in Martin-Löf Type Theory (Bishop Set Theory). Our categorical description of dependency is an extension of earlier work of Pitts. Namely, we describe the type-categories of Pitts as categories with family-arrows and Sigma-objects, and we introduce categories with dependent arrows, or dep-categories, independently from Sigma-objects. The existence of dependent arrows in a dep-category affects the definition of the corresponding Sigma-structure, as the second-projections, which are appropriate dependent arrows, are crucially involved in the definition of the new Sigma-objects. All concepts and results concerning the above categories can be dualized.
Pitts described only the canonical family arrows on a topos. Here we describe the corresponding canonical Sigma-structure and the canonical dep-structure on a topos, together with their 2-categorical versions (this part of our presentation is joint work with Yannick Ehrhardt). All these concepts and all related results on toposes can be dualised, and the canonical cofamily arrows, coSigma-objects, and codependent arrows on toposes emerge in a natural manner.
Elio Pivet (Grothendieck Institute and ETH Zurich)
The theory of categories enriched in a monoidal category is well-known, and it has been shown that it can be extended to a theory of enrichment in bicategories. Quantaloids are a particular case of bicategories, and it has been shown that the theory of categories enriched in a quantaloid generalizes that of sheaves over a locale, and even recovers the case of sheaves over a site as a particular case.
We will present the general definitions for sheaves enriched in a bicategory, and extend some definitions from quantaloid enrichment theory to the general case of a fixed bicategory. This will enable us to define a particular category of enriched categories which plays the role of the category of sheaves over the base bicategory. This theory recovers simultaneously the case of sheaves over quantaloids and that of sheaves over sites.
In general, such categories are not Grothendieck toposes (it was already the case for general quantaloids), but they can be seen as reflexive subcategories of categories of presheaves in a suitable sense. As these objects are more general than toposes, we call them B-toposes (B denoting the generic name for a bicategory).
This is joint work with Olivia Caramello.
Fabian Ruch
(Göteborgs Universitet)
Logics as Kan Injectivity Classes of Toposes
The aim of this talk is to define the notion of (fragment of geometric) logic using the technology of Kan injectivity introduced by Di Liberti, Lobbia and Sousa. We shall show that many relevant fragments of geometric logic can be described as injectivity classes, thus offering a good framework to describe various logics under this pattern.
We first recall the right Kan injectivity of algebraic toposes with respect to all geometric morphisms. We then recall the right Kan injectivity of coherent toposes with respect to flat geometric morphisms. Lastly, we present right Kan injectivity properties of localic toposes, locally decidable toposes, regular toposes and disjunctive toposes.
Ivan Tomasic (Queen Mary University of London)
Galois theory of differential schemes
Since 1883, Picard-Vessiot theory had been developed as the Galois theory of differential field extensions associated to linear differential equations.
Inspired by categorical Galois theory of Janelidze, and by using novel methods of precategorical descent applied to algebraic-geometric situations related to differential schemes viewed as precategory actions, we develop a Galois theory that applies to morphisms of differential schemes, and vastly generalises the linear Picard-Vessiot theory, as well as the strongly normal theory of Kolchin.
Davide Trotta (University of Padua)
Presheaves, Sheaves and Sheafification via triposes
The notion of tripos was originally introduced by Hyland, Johnstone and Pitts to explain from an abstract perspective in which sense localic sheaf toposes and Hyland’s realizability toposes are instances of the same construction.
The main purpose of this work is to further investigate the common structures of these classes of toposes from a more geometric point of view. In particular, we first introduce an exact category of “abstract presheaves” for (arbitrary-based) triposes by combining the tripos-to-topos construction with the full existential completion. The given name is motivated by the fact that abstract presheaves coincide with localic presheaves in the case of localic triposes. Then, we call ∃-sheaf triposes those triposes whose abstract presheaves category is a topos, and we prove that every Set-based tripos is a ∃-sheaf tripos.
Furthermore, we show that the sheafification between a localic topos and its presheaf topos can be generalized to an “abstract sheafication adjunction” between a ∃-sheaf triposes and its full existential completion. In particular, we conclude that any tripos-to-topos construction of a Set-based tripos can be seen as the category of j-sheaves for the Lawvere-Tierney topology j induced by an abstract sheafication adjunction.
This talk is based on joint work with Maria Emilia Maietti.
Joshua Wrigley (Queen Mary University of London)
A groupoidal classification of theories via topos theory
There has been renewed interest within the model theory community in the question of whether a logical theory can be characterised by the symmetries of (a set of) its models, endowed with some further topological data. The first appearance in the literature of this kind of result is a paper of Ahlbrandt and Ziegler (“Quasi finitely axiomatizable totally categorical theories,” Annals of Pure and Applied Logic, vol. 30, no. 1, pp. 63–82, 1986), where it is shown that a countably categorical theory is characterised, up to bi-interpretability, by the topological automorphism group of its unique countable model. Recently, Ben Yaacov (“Reconstruction of non-ℵ0-categorical theories,” Journal of Symbolic Logic, vol. 87, no. 1, pp. 159–187, 2022) has shown that the countable categoricity assumption can be dropped if we instead work with topological groupoids (though his groupoids are not groupoids of models).
We will present a topos-theoretic approach to this problem by associating topoi to both logical and topological/algebraic data. Each logical theory has a classifying topos, which characterises the theory up to Morita equivalence (a mild generalisation of bi-interpretability, see McEldowney, “On Morita equivalence and interpretability,” Review of Symbolic Logic, vol. 13, no. 2, pp. 388–415, 2020), while a topological groupoid generates a topos of equivariant sheaves.
We will identify when the topos of sheaves on an open topological groupoid of models classifies a logical theory, and when two such groupoids have equivalent topoi of sheaves, extending the classical result of Ahlbrandt and Ziegler.
Fernando Yamauti (University of São Paulo and University of Regensburg)
Some Properties of some Homotopy Theories of Topoi
Homotopy theory in a topos is a relatively well developed topic be it from the point of view of test topoi or the homotopy theory internal to a (higher) topos. Nevertheless, the homotopy theory of the category of (higher) topoi itself was not well explored in the literature. Following the historical developments since Grothendieck’s Galois theory, one is tempted to use shape theory as the main homotopy theoretical invariant attached to a topos. Still, much of shape theory is only known after profinite completion, after which much of the theory is completely simplified.
Coming from a completely different side, one is yet also confronted before another possible homotopy theory. For every choice of an interval object inside the category of topoi, one can define suitable notions of n-connectedness taking into account the possible lack of points in a topos. Natural candidates for intervals are the Sierpiński interval and the ordinary topological interval.
In this talk, I intend to talk about ongoing work on the relation between those two flavours of homotopy theory. If time permits, I shall also comment on related work in progress towards the extension of Joyal-Tierney’s paradigm of “topos as localic stacks” to higher topoi.
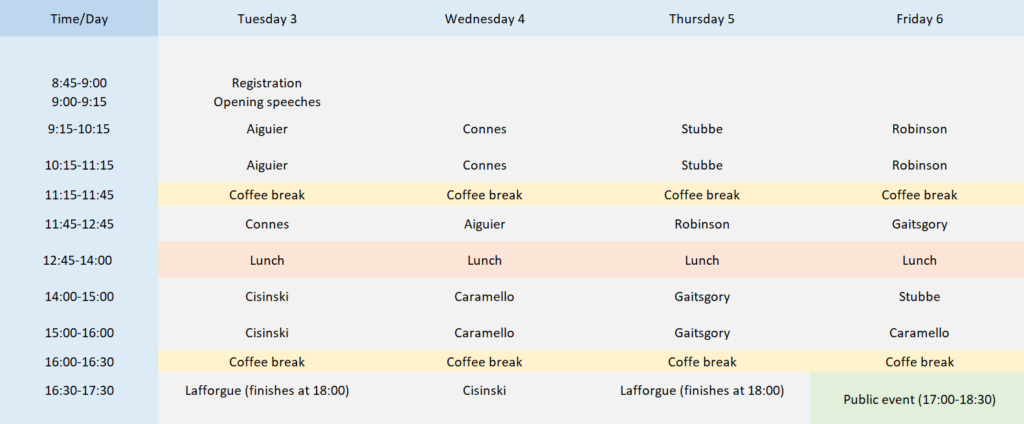
School timetable
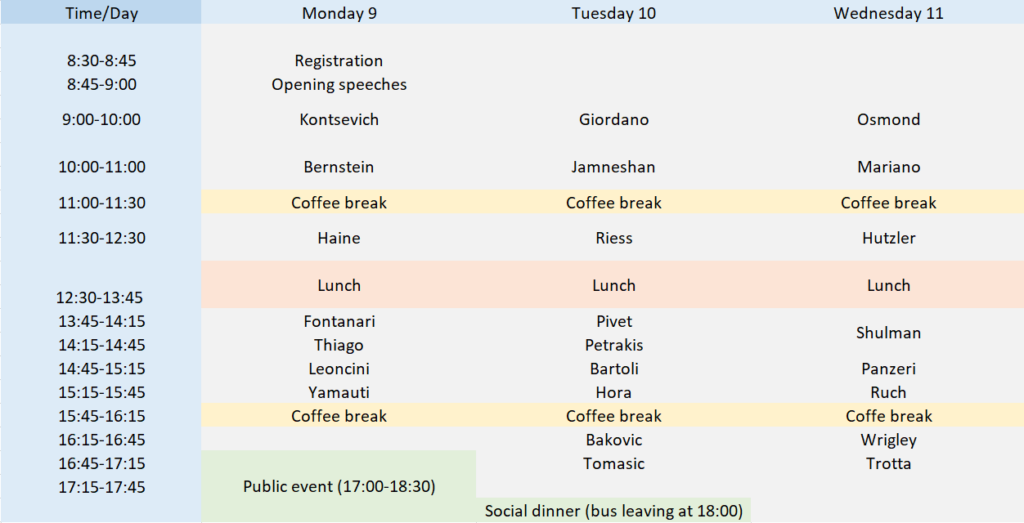
Conference timetable
Two events for the general public
As part of the social programme of “Toposes in Mondovì” (3-11 September 2024), the Grothendieck Institute organizes two events for the general public (held in Italian), to explore the relations between mathematics and other disciplines, notably literature and music.
The event “La ricerca dell’universale, tra matematica e letteratura” (6 September), with the participation of Laurent Lafforgue, Alain Connes, well known writer Gianrico Carofiglio and mathematician and science disseminator Claudio Bartocci, will propose a dialogue between mathematics and literature around the theme of universality and Grothendieck’s views on it.
The lecture-concert “Topoi e motivi, tra matematica e musica” (9 September), organized in collaboration with the renowned baroque orchestra Academia Montis Regalis, will instead explore the relations between mathematics and music: Olivia Caramello and harpsichordist and conductor Chiara Cattani will exchange around the theme of symmetries and of the creation of forms from a unity, explaining its relevance both for mathematics and baroque music. To illustrate the principles covered in the lesson, pieces by Bach, Corelli, Sammartini and Vivaldi will be performed.
Registration is free but compulsory, and must be made by compiling the form available at this page.
Visit to the Sanctuary of Vicoforte and social dinner
In the evening of 10 September, participants in “Toposes in Mondovì” will be able to join a guided visit
(in English) to the magnificent Sanctuary of Vicoforte, internationally renowned for its dome, which is the largest elliptical in the world.
A bus for Vicoforte will depart from Mondovì Piazza, near the conference site, at 18:00. The visit of the Sanctuary will begin at 18:30 and will last approximately 45 minutes. It will be followed by a dinner in two parts at the nearby complex Casa Regina Montis Regalis: the first part will have the form of a buffet taking place in the beautiful gardens of Casa Regina overlooking the Sanctuary, while the second part, consisting of the main dish and a dessert, will take place in the interiors. The bus will bring participants back to Mondovì at 23:00, with stops both in Mondovì Piazza and in the lower part of Mondovì.
If you wish to take part in this activity, please register by filling the following form and pay the corresponding fee (of 40 euros) before the 2nd of September.

The following is the final list of participants to “Toposes in Mondovì” :
N. | Name | Affiliation | Country |
| 1 | Gabriel Aaron Saadia | Stockholm University | Sweden |
| 2 | Marc Aiguier | CentraleSupélec, Université Paris-Saclay | France |
| 3 | Mohamed Alaoui | Cultydata | France |
| 4 | Thiago Alexandre | University of São Paulo and IMJ, Paris | Brazil/France |
| 5 | Daniel Almeida | University of Ottawa | Canada |
| 6 | Quentin Aristote | IRIF, Université Paris-Cité and INRIA PiCube | France |
| 7 | Peter Arndt | University of Duesseldorf | Germany |
| 8 | Igor Baković | Independent | Croatia |
| 9 | Léo Bartoli | Grothendieck Institute and ETH Zurich | Italy/Switzerland |
| 10 | Frédéric Berlioz | Cerema | France |
| 11 | Joseph Bernstein | Tel Aviv University | Israel |
| 12 | Paolo Bertozzini | Thammasat University | Thailand |
| 13 | Noa Bihlmaier | University of Tuebingen | Germany |
| 14 | Anthony Bordg | Huawei | France |
| 15 | Lilian Bost | Aix Marseille Université | France |
| 16 | Samuel Bourgeat | EPFL, GR-JAKSIC | Switzerland |
| 17 | JJacques Brahim | Aix Marseille Université | France |
| 18 | Guillaume Bressan | Université d’Artois | France |
| 19 | Daniel Buis | Independent | France |
| 20 | Alain Cagnati | Independent | France |
| 21 | Olivia Caramello | University of Insubria and Grothendieck Institute | Italy |
| 22 | Carles Casacuberta | Universitat de Barcelona | Spain |
| 23 | Marine Cases | Sorbonne Université | France |
| 24 | Franco Cazzaniga | University of Insubria | Italy |
| 25 | Yorgo Chamoun | École Polytechnique | France |
| 26 | Russi Chatterjee | Independent | India |
| 27 | Federico Ciliegi | University of Padua | Italy |
| 28 | Denis-Charles Cisinski | University of Regensburg | Germany |
| 29 | Alain Connes | IHES | France |
| 30 | Virgile Constantin | EPFL | Switzerland |
| 31 | Nathan Corbyn | University of Oxford | United Kingdom |
| 32 | Gabriele D’Acunto | CENTAI Institute | Italy |
| 33 | Julien Dalpayrat-Glutron | UQAM – Université du Québec à Montréal | Canada |
| 34 | Arnav Das | Caltech | USA |
| 35 | Mayk de Andrade | University of São Paulo | Brazil |
| 36 | Pablo Donato | Grothendieck Institute | Italy |
| 37 | Bruno Drieux | École Polytechnique | France |
| 38 | Xuanrui Fan | Ecole Polytechnique | France |
| 39 | Renato Faraone | University of Parma | Italy |
| 40 | Tomás Fernández | École Normale Supérieure de Lyon | France |
| 41 | Claudio Fontanari | University of Trento | Italy |
| 42 | Dennis Gaitsgory | Max Planck Institute for Mathematics | Germany |
| 43 | Guillaume Geoffroy | Université Claude-Bernard Lyon 1 | France |
| 44 | Paolo Giordano | University of Vienna | Austria |
| 45 | Arnold Grigorian | NRU HSE | Russia |
| 46 | Paul Grosskopf | Université Libre de Bruxelles | Belgium |
| 47 | Lucy Grossman | Université catholique de Louvain | Belgium |
| 48 | Marc Groz | University of Connecticut | USA |
| 49 | Peter Haine | University of California, Berkeley | USA |
| 50 | François Hantry | Amadeus | France |
| 51 | Ryuya Hora | University of Tokyo | Japan |
| 52 | Keisuke Hoshino | Kyoto University | Japan |
| 53 | Matthias Hutzler | University of Gothenburg | Sweden |
| 54 | Asgar Jamneshan | Koç University | Turkey |
| 55 | Vít Jelínek | Masaryk University, Brno | Czech Republic |
| 56 | Moana Jubert | Inria, IRIF, CNRS, Université Paris-Cité | France |
| 57 | Maxim Kontsevich | IHES | France |
| 58 | Laurent Lafforgue | Huawei | France |
| 59 | Raffaele Lamagna | Grothendieck Institute and CentraleSupélec, Université Paris-Saclay | Italy/France |
| 60 | Samuel Lavenir | EPFL | Switzerland |
| 61 | Jaehyeok Lee | Pohang University of Science and Technology | South Korea |
| 62 | Georg Lehner | Freie Universität Berlin | Germany |
| 63 | Giuseppe Leoncini | Masaryk University & University of Milano | Czech Republic/Italy |
| 64 | Fabrizio Leopardi | Unige | Italy |
| 65 | Dominique Lepetz | École des mines | France |
| 66 | Yaxin Li | University of Melbourne | Australia |
| 67 | Elsa Lubek | École Polytechnique | France |
| 68 | Hugo Luiz Mariano | University of São Paulo | Brazil |
| 69 | Bernardo Martins | Instituto Superior Técnico | Portugal |
| 70 | Iskander Mathews | University of Edinburgh | United Kingdom |
| 71 | Paul-André Mellies | IRIF, CNRS | France |
| 72 | Gabriel Merlin | Grothendieck Institute and CentraleSupélec, Université Paris-Saclay | Italy/France |
| 73 | Meha Mishra | University of Petroleum and Energy Studies | India |
| 74 | Kira Morozova | Universidade de Aveiro | Portugal |
| 75 | Ruben Mud | Independent | The Netherlands |
| 76 | Marcus Nicolas | LMU and Université d’Artois | France |
| 77 | Axel Osmond | Grothendieck Institute | Italy |
| 78 | Marcella Palese | University of Turin | Italy |
| 79 | Fidèle Palouki | Independent | France |
| 80 | Marco Panzeri | University of Insubria | Italy |
| 81 | Federica Pasqualone | Carnegie Mellon University | USA |
| 82 | Susana Patiño Espinosa | ITAM | Mexico |
| 83 | Iosif Petrakis | University of Verona | Italy |
| 84 | Wilma Pilati | University of Trento | Italy |
| 85 | Jannik Pitt | Julius-Maximilians-Universität Würzburg | Germany |
| 86 | Elio Pivet | Grothendieck Institute and ETH Zurich | Italy/Switzerland |
| 87 | Hans Riess | Duke University | USA |
| 88 | Silvio Rini | University of Pisa | Italy |
| 89 | Michael Robinson | American University | USA |
| 90 | Fabian Ruch | Göteborgs Universitet | Sweden |
| 91 | Nick Ruoff | University of Tübingen | Germany |
| 92 | Owen Sabatin | Sorbonne université | France |
| 93 | Aurélien Sagnier | Huawei | France |
| 94 | Simone Sartori | University of Turin | Italy |
| 95 | Johannes Schipp von Branitz | University of Nottingham | United Kingdom |
| 96 | Zhan Shi | Kyushu University, Joint Graduate School of Mathematics for Innovation | Japan |
| 97 | Zev Shirazi | University of Oxford | United Kingdom |
| 98 | Michael Shulman | University of San Diego | USA |
| 99 | Anny Beatriz Silva de Azevedo | University of São Paulo | Brazil |
| 100 | Alain Simon | Independent | France |
| 101 | Devon Stockall | University of Southern Denmark | Denmark |
| 102 | Isar Stubbe | Université du Littoral-Côte d’Opale | France |
| 103 | Tianjian Tan | Sorbonne Université | France |
| 104 | Francesco Tognetti | University of Padua | Italy |
| 105 | Ivan Tomasic | Queen Mary University of London | United Kingdom |
| 106 | Davide Trotta | University of Padua | Italy |
| 107 | Gabriel Tubio | Independent | Germany |
| 108 | Berend Van Starkenburg | Leiden University | The Netherlands |
| 109 | Corentin Vienne | Université catholique de Louvain | Belgium |
| 110 | Jinyi Wang | Tsinghua University | China |
| 111 | Ekkehart Winterroth | University of Turin | Italy |
| 112 | Hartwig Winterroth | University of Turin | Italy |
| 113 | Michael Wright | The Archive Trust for Mathematical Sciences and Philosophy | United Kingdom |
| 114 | Joshua Wrigley | Queen Mary University of London | United Kingdom |
| 115 | Yiqi Xu | Universität Stuttgart | Germany |
| 116 | Luqiao Xu | Johns Hopkins University | USA |
| 117 | Fernando Yamauti | University of São Paulo and University of Regensburg | Brazil/Germany |
| 118 | Junche Yu | Université du Littoral-Côte d’Opale | France |
| 119 | Errol Yuksel | Stockholm University | Sweden |
| 120 | Alexander Zahrer | University of Graz | Austria |
| 121 | Alexander Zenkovich | École Normale Supérieure de Paris | France |
We thank the following institutions or individuals for their collaboration in the context of the organization of “Toposes in Mondovì” and the associated events:

Do you want to know more about the Grothendieck Institute?
Subscribe to our Newsletter
Istituto Grothendieck ETS
- Corso Statuto 24
12084 Mondovì CN – Italy - Fiscal Code: 93062550046
- Registered at RUNTS rep. n. 26177
DDR Piemonte n. 577 del 04.04.2022
Contacts
- Phone: +39 0174 082040
- E-mail: info@igrothendieck.org
- PEC: igrothendieck@pec.it















